关于简谐运动周期公式的简单推导(不超纲)
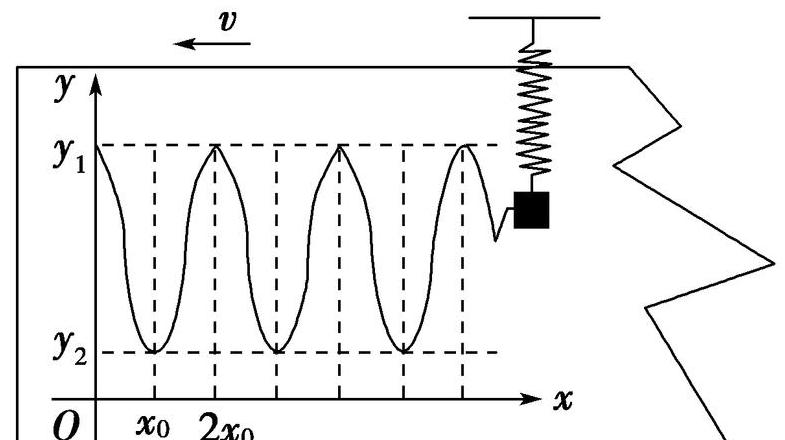
在探讨简谐运动的周期公式时,我们主要借助两种模型——弹簧振子和单摆——来进行推导。首先,对于弹簧振子,核心的物理关联是弹簧的回复力F与位移x的比例关系,即F=kx,这里k代表弹簧的刚度系数。
结合牛顿第二定律F=ma,其中m是质量,a是加速度,我们可以通过联立这两个方程来得到ma=kx。
进一步,通过将加速度a表示为位移的二阶导数(即a=d²x/dt²),并将其代入上述方程,解出这个二阶微分方程,便可得出简谐运动的周期公式:T=2 π√(m/k)。
其次,针对单摆,当摆角极小的情况下,单摆的回复力F可以近似视为重力在摆角方向上的分量,即F=mgsinθ≈mgθ。
将这个关系代入简谐运动的基本公式中,经过相似的推导步骤,我们同样可以得到单摆的周期公式:T=2 π√(l/g),其中l为摆长,g为重力加速度。
尽管简谐运动的周期公式在不同的系统中有其特定的表达形式,但其推导均根植于一致的物理原理。
高中物理请写出弹簧振子周期公式的证明过程T2mk
弹簧振子的周期计算方式为 T = 2 π√(m/k),这里 T 代表周期,m 指振子的质量,k 则是弹簧的劲度系数。要推导这个公式,可以按以下步骤进行:
1 . 首先,把弹簧振子的运动看作是简谐运动的一种表现,它的运动方程是 x''(t) + (k/m)x(t) = 0,其中 x(t) 是位移,x''(t) 是位移的二阶导数,也就是加速度。
2 . 解这个方程你会得到一个正弦函数的形式,即 x(t) = Acos(ωt+φ),其中 A 是振幅,ω 是角频率,φ 是初相位。
3 . 角频率 ω 是由弹簧的劲度系数 k 和振子的质量 m 决定的,具体关系是 ω = √(k/m)。
4 . 周期 T 实际上是角频率 ω 的倒数乘以 2 π,即 T = 2 π/ω。
5 . 把 ω 的表达式代入到 T 的公式中,最终得到 T = 2 π√(m/k)。
这个公式清楚地展示了弹簧振子的周期仅仅取决于振子的质量 m 和弹簧的劲度系数 k,而与振幅 A 和初相位 φ 无关。
高中物理:请写出弹簧振子周期公式的证明过程(T=2π√(m/k))
弹簧振子的周期计算公式为T=2 π√(m/k),下面是这一公式的推导思路:1 . 在理想情况下,弹簧振子的机械能保持不变,即动能与势能之和恒定。
机械能由动能和势能构成。
2 . 动能的公式是E=mv²/2 ,其中v为振子的速度。
结合简谐振动的位移公式x=asin(ωt),通过求导可得速度表达式v=dx/dt=acos(ωt)。
3 . 将速度表达式代入动能公式,得到E=m(a cos(ωt))²/2 =ma² cos²(ωt)/2 由于振子通过同一位置时速度方向可能相反,动能也可表示为E=ma²ω²/2 ,其中ω为圆频率,ω=2 πf,f为振动频率。
4 . 势能的公式为P=kx²/2 ,其中k为弹簧劲度系数,x为位移。
将位移表达式代入,得到P=k(a sin(ωt))²/2 =ka² sin²(ωt)/2
5 . 由于机械能守恒,动能与势能相等,即E=P。
将动能和势能的表达式等式化,得到ma²ω²/2 =ka² sin²(ωt)/2
6 . 解该方程可得ω²=k/m,即ω=√(k/m)。
7 . 周期T与频率f互为倒数,T=1 /f。
结合ω与T的关系,T=2 π/ω=2 π/√(k/m)。
8 . 最终化简得到T=2 π√(m/k),这就是弹簧振子的周期公式。