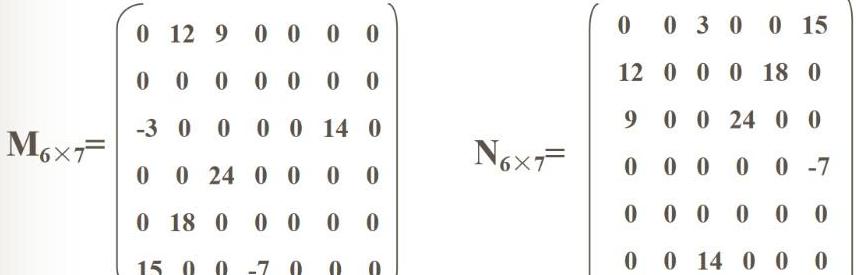对稀疏矩阵进行压缩存储的目的是什么?
压缩存储稀疏矩阵的核心目标在于降低存储消耗。传统上,矩阵的存储常以二维数组形式进行,此方法便于随机访问任意元素,便于执行矩阵运算。
然而,对于稀疏矩阵,若继续采用这种二维数组方式,则会大量冗余地存储零元素,导致空间浪费,并增加处理零元素的计算负担。
因此,针对稀疏矩阵,实施压缩存储策略变得尤为必要。
此外,稀疏矩阵在计算效率上具有显著优势,特别是在MATLAB中,它仅针对非零元素进行操作,这一特性是稀疏矩阵的显著优点。
例如,对于相同矩阵A和B,执行2 A可能需要一百万次浮点运算,而2 B则仅需2 000次。
由于MATLAB不支持自动生成稀疏矩阵,用户需使用特定命令来构建。
稀疏矩阵支持算术和逻辑运算。
以二维数组形式存储的稀疏矩阵Amn,若每个元素占用L字节,则整个矩阵的存储空间为mnL字节。
存储矩阵是什么结构
矩阵数据通常借助专门的存储结构来管理,这种结构就是存储矩阵。矩阵本质上是一种多维数组,由行和列的元素构成。
在存储矩阵时,主要采用两种策略:顺序存储和压缩存储。
前者利用二维数组来存放数据,每个元素的位置都是固定的,通过行列索引就能轻松找到,对于一般的线性矩阵来说,这种方式既简单又明了。
而后者则针对一些特殊的矩阵,比如对称矩阵和上(下)三角矩阵,进行特别设计。
对称矩阵以其主对角线为轴对称,所以只需要存储一侧的数据即可,用一维数组就足够了。
同样,上(下)三角矩阵也只需要存储主对角线以下(或以上)的元素,这样可以大大节省存储空间。
选择哪种存储结构,主要还是看矩阵本身的特性和存储需求,对于普通的线性矩阵,顺序存储是不错的选择,而对于那些特殊的矩阵,压缩存储则更为高效。