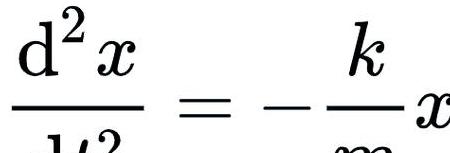弹簧振子简谐运动总能量公式

一质量为m以v(t)=v0sinwt的规律运动，则振动系统的总机械能为

一个进行简谐运动的系统，其机械能是势能与动能的总和。
当速度为V0时，系统的势能为零，因此总机械能就等于动能，即（1 /2 ）mv0^2 在分析加速度a时，我们可以通过F=Ma得出a=F/M，并且有a=at，其中t表示时间。
进一步推导可以得到a=Ft/M。
功率P则可以通过力F与速度Vt的乘积来表示，即P=FVt，也可以写成P=(F^2 )t/M，这里的(F^2 )指的是力F的平方。

关于简谐运动的圆频率，它是由系统的力学特性决定的，因此也被称为固有圆频率。
以弹簧振子为例，其圆频率的公式为ω=√(k/m)，其中k代表弹簧的刚度系数，m代表振子的质量。
对于一个特定的弹簧振子，其圆频率只取决于弹簧的刚度和质量，是系统本身固有属性的表现。

参考资料来源于百度百科对简谐运动的介绍。

简谐运动的回复力和能量

一、简谐运动的回复力概览 1 . 当质点所受力与其从平衡点偏离的位移成正比，且作用方向始终指向平衡点时，其运动即构成简谐运动。
2 . 回复力，即推动振动物体回归平衡点的力。
3 . 回复力始终朝向平衡点。
4 . 回复力的数学表达为F=-kx，此式揭示回复力与位移成正比，负号意味着力的方向与位移方向相反，k为系统特定的常数。

二、简谐运动的能量动态 1 . 弹簧振子的运动涉及动能与势能的转换。
（1 ）当位移达到极值时，势能最大，动能降至零。
（2 ）通过平衡位置时，动能达峰值，而势能最小。
2 . 简谐运动的能量属性在于系统机械能的守恒，尽管实际过程中存在能量耗散，简谐运动仍被视为一个理论上的理想模型。

怎样计算作简谐振动的弹簧振子的能量

弹簧振子的总能量，可以用E=1 /2 KA² 这个公式来算，K代表弹簧的劲度系数，A则是振动的最大幅度。
另外，依据机械能守恒，能量还能写成E=1 /2 mVm² ，m是振子的质量，Vm是振子经过平衡点时的速度。
这两种计算方法不仅适用于简单的简谐振动，对探究更复杂的物理现象也很有用。

简谐振动属于周期性运动，它的特点是受力方向总是指向平衡点，并且力的大小与位移成正比。
依照胡克定律，回复力F可以表示为F=-kx，其中k是力和位移之间的比例常数，需要注意的是，k和弹簧的劲度系数不是一回事，这里的负号说明回复力的方向总是和位移方向相反。

简谐振动的周期T可以用T=2 π√（m/k）来计算，m是振子的质量，k是振动系统的回复力系数。
对于单摆运动，周期T的公式是T=2 π√（L/g），L是摆长，g是重力加速度。
从这个公式我们可以推导出g=(4 π² ×L)/(T² )，并且可以通过实验来测定某个地方的重力加速度。

值得一提的是，简谐振动的周期并不受振幅（当偏角小于1 0度时）和摆球质量的影响。
当偏角小于1 0度时，我们可以近似认为sina≈a，这里的a是弧度，也就是振动轨迹的弧长除以摆长，近似等于位移x除以L。
此时回复力F回=-mg/Lx。
依照牛顿第二定律，F=ma，运动物体的加速度和所受合力的大小成正比，方向相同。
这种基础的数学模型能帮助我们更清楚地认识复杂物理现象背后的规律。